Lithophanie sur des supports incurvés

Ooooolà la communauté Dyrkienne,
J’ai eu le plaisir de vous proposer récemment un article sur la conception de lithophane (https://dyrk.org/2025/06/14/format-stl-et-lithophanie/), avec en prime un petite code Javascript vous permettant de créer vos propres lithophanies imprimables si vous avez une imprimantes 3D ou un copain qui en a une.
Cet article était alors une mise en bouche :
A la fois sur la découverte du format « STL » et des ses fameux triangles, mais également sur l’explication théorique et pratique de ce qu’est un Lithophane.
Nous allons désormais approfondir un peu le sujet …
Lithophane à plat
Créer un petit Lithophane à plat, ne demande pas forcément de faire des Maths, on parcourt simplement les pixel d’une image en X et Y …
Et on génère des cubes sur ces mêmes coordonnées, en ajustant un la hauteur sur Z…
Enfin presque !
Attention, 3,2, 1, retournement de cerveau.
Notre Lithophane est à plat, donc X et Y sont simplement à permuter en X et Z.
Et la Hauteur, calculé en fonction du contraste du pixel, devient Y.
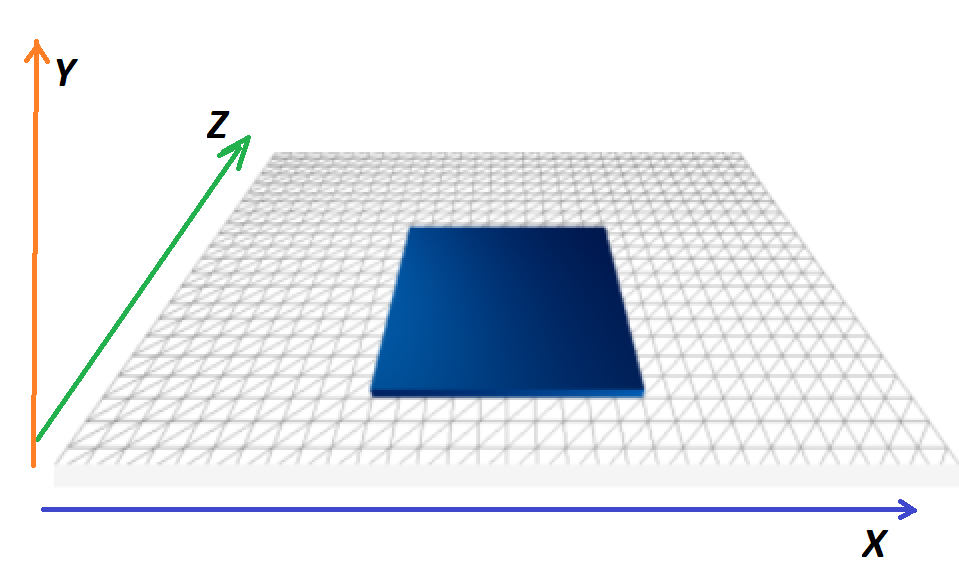
Ainsi donc, les coordonnées sont plus ou moins indiqués, on lit une image pixel par pixel, et on génère notre lithophanie en positionnant
au même endroit les pixels en remplaçant les coordonnées X, Y d’une image en X, Z.
Quant au Y on est sur du plat, donc tout les cubes positionnés partent du même endroit en Y = 0 et sont ajusté en hauteur Y = (n) selon la couleur du pixel.
Lithophanie et support incurvé.
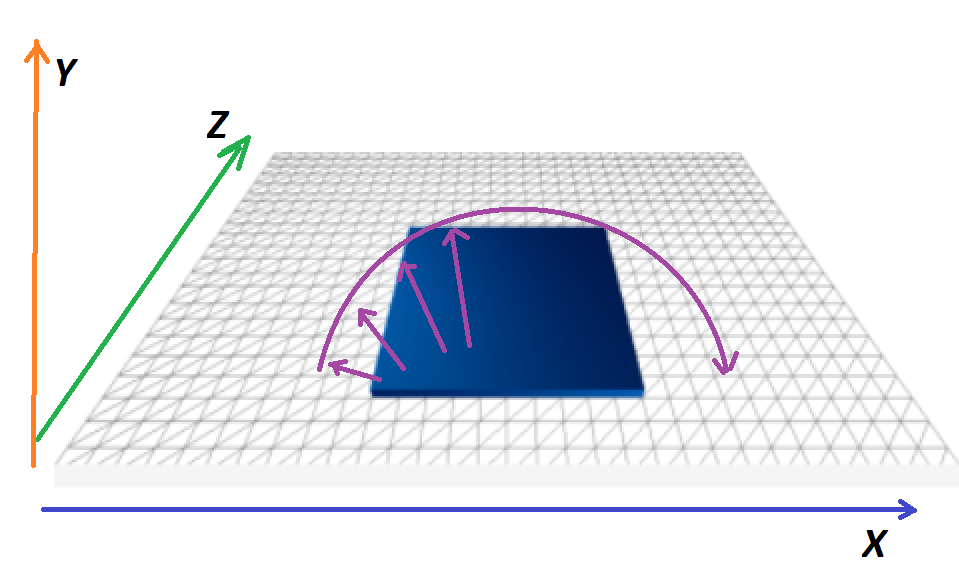
Ici, il faut bien évidemment continuer à balayer les pixels de notre image, mais nous devons positionner nos petits cubes, sur une courbe.
J’ai donc fait un peu de trigonométrie.
Comme sur le support « plat », je vais prendre mon imageet la parcourir en X, Y pixel par pixel.
Cela me permet de déterminer la « hauteur / profondeur » du pixel.
Z ne bougera pas car la hauteur de l’image ne change pas.
mais nous allons recalculer x et y selon la formule suivante.
x = *radius x cosinus(PI x *degree / 180)
y = *radius x sinus(PI x *degree / 180)
* radius :
Tout simplement le rayon, plus cette valeur est élevée, plus la courbe sera grande.
*degree :
En parcourant l’image en X, cette valeur change de façon incrémentale.
L’idée c’est de calculer cette valeur en fonction de X et de la valeur de l’angle.
Pour cela on fait des pourcentage avec un tableau en croix.
percentX = X (position du pixel de l’image) x 100 / ImageWidth (taille de l’image)
degree = percentX * Angle / 100
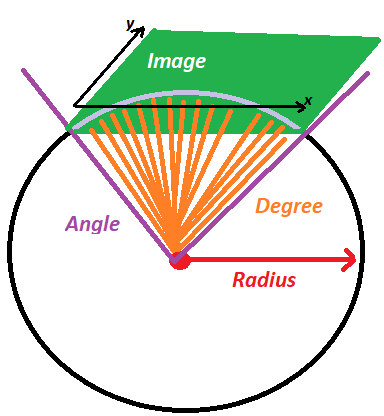
Ainsi cette formule, permet de déterminer la position en Y ou positionner notre pixel (cube).
A cette valeur, il faut ajouter également la hauteur de notre pixel qu’on calcule en fonction du contraste.
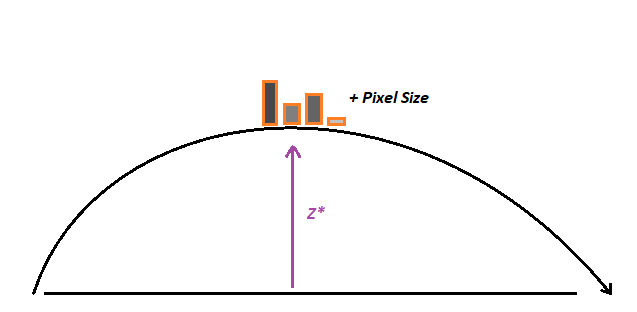
Eh voilà, avec un peu de trigonométrie, vous êtes désormais en mesure de calculer à la fois, X et Y … Z ne changeant pas (position Y du pixel de l’image).
Code Javascript
Comme dans la plupart de mes articles, voici un bout de code que vous pourrez directement exécuter depuis la console de votre navigateur
et qui fera le job pour vous, afin de générer des Lithophanes « incurvés ».
Comme d’habitude, il vous suffit d’ouvrir la console de votre navigateur (touche F12 de votre clavier), puis depuis celle-ci d’aller sur un onglet « console », et de copier-coller le contenu ci-dessous.
Enfin, validez avec la touche entrée.
A présente vous devriez disposer d’une interface pour sélectionner l’image que vous souhaitez convertir en lithophanie incurvé.
html = document.getElementsByTagName('body')[0];
/*********************************************
Control Panel
***********************************************/
descriptionSupportCheckBox = document.createElement('span');
descriptionSupportCheckBox.textContent = 'Ajouter un support carré';
addSupportCheckbox = document.createElement('input');
addSupportCheckbox.type='checkbox';
addSupportCheckbox.checked = true;
descriptionMaxWidthInput = document.createElement('span');
descriptionMaxWidthInput.textContent = 'Largeur Max';
maxWidthInput = document.createElement('input');
maxWidthInput.value = 250;
Number.prototype.toFixed2 = Number.prototype.toFixed2 ? Number.prototype.toFixed2 : Number.prototype.toFixed;
Number.prototype.toFixed = function(x){
x = Number(x);
if (this.valueOf() % 1 == 0 || this.valueOf() % 1 == -0) return this.valueOf();
return this.toFixed2(x);
};
function generateAsciiStlLitophanie(){
buff = "solid litophanie\n";
downloadFile = document.createElement('a');
img = document.getElementsByTagName('img')[0];
canvas = document.createElement('canvas');
canvas.width = Math.min(img.naturalWidth, maxWidthInput.value > 0 ? maxWidthInput.value : 250);
canvas.height = (img.naturalHeight * 100 / img.naturalWidth) * canvas.width / 100;
canvas.ctx = canvas.getContext('2d');
canvas.ctx.translate(canvas.width, 0);
canvas.ctx.scale(-1, 1);
canvas.ctx.drawImage(img, 0, 0, img.naturalWidth, img.naturalHeight,
0, 0, canvas.width, canvas.height);
html.append(canvas);
createCube = (fromZ, x, y, z, w, h) => {
return `facet normal 0 0 -1
outer loop
vertex ${x.toFixed(2)} ${y.toFixed(2)} ${fromZ}
vertex ${(x+w).toFixed(2)} ${y.toFixed(2)} ${fromZ}
vertex ${(x+w).toFixed(2)} ${(y+h).toFixed(2)} ${fromZ}
endloop
endfacet
facet normal 0 0 -1
outer loop
vertex ${x.toFixed(2)} ${y.toFixed(2)} ${fromZ}
vertex ${(x+w).toFixed(2)} ${(y+h).toFixed(2)} ${fromZ}
vertex ${x.toFixed(2)} ${(y+h).toFixed(2)} ${fromZ}
endloop
endfacet
facet normal 0 0 1
outer loop
vertex ${x.toFixed(2)} ${(y).toFixed(2)} ${z.toFixed(2)}
vertex ${x.toFixed(2)} ${(y+h).toFixed(2)} ${z.toFixed(2)}
vertex ${(x+w).toFixed(2)} ${(y+h).toFixed(2)} ${z.toFixed(2)}
endloop
endfacet
facet normal 0 0 1
outer loop
vertex ${x.toFixed(2)} ${y.toFixed(2)} ${z.toFixed(2)}
vertex ${(x+w).toFixed(2)} ${(y+h).toFixed(2)} ${z.toFixed(2)}
vertex ${(x+w).toFixed(2)} ${y.toFixed(2)} ${z.toFixed(2)}
endloop
endfacet
facet normal 0 -1 0
outer loop
vertex ${x.toFixed(2)} ${y.toFixed(2)} ${fromZ}
vertex ${x.toFixed(2)} ${y.toFixed(2)} ${z.toFixed(2)}
vertex ${(x+w).toFixed(2)} ${y.toFixed(2)} ${z.toFixed(2)}
endloop
endfacet
facet normal 0 -1 0
outer loop
vertex ${x.toFixed(2)} ${y.toFixed(2)} ${fromZ}
vertex ${(x+w).toFixed(2)} ${y.toFixed(2)} ${z.toFixed(2)}
vertex ${(x+w).toFixed(2)} ${y.toFixed(2)} ${fromZ}
endloop
endfacet
facet normal 0 1 0
outer loop
vertex ${x.toFixed(2)} ${(y+h).toFixed(2)} ${fromZ}
vertex ${(x+w).toFixed(2)} ${(y+h).toFixed(2)} ${fromZ}
vertex ${(x+w).toFixed(2)} ${(y+h).toFixed(2)} ${z.toFixed(2)}
endloop
endfacet
facet normal 0 1 0
outer loop
vertex ${x.toFixed(2)} ${(y+h).toFixed(2)} ${fromZ}
vertex ${(x+w).toFixed(2)} ${(y+h).toFixed(2)} ${z.toFixed(2)}
vertex ${x.toFixed(2)} ${(y+h).toFixed(2)} ${z.toFixed(2)}
endloop
endfacet
facet normal -1 0 0
outer loop
vertex ${x.toFixed(2)} ${y.toFixed(2)} ${fromZ}
vertex ${x.toFixed(2)} ${(y+h).toFixed(2)} ${fromZ}
vertex ${x.toFixed(2)} ${(y+h).toFixed(2)} ${z.toFixed(2)}
endloop
endfacet
facet normal -1 0 0
outer loop
vertex ${x.toFixed(2)} ${y.toFixed(2)} ${fromZ}
vertex ${x.toFixed(2)} ${(y+h).toFixed(2)} ${z.toFixed(2)}
vertex ${x.toFixed(2)} ${y.toFixed(2)} ${z.toFixed(2)}
endloop
endfacet
facet normal 1 0 0
outer loop
vertex ${(x+w).toFixed(2)} ${y.toFixed(2)} ${fromZ}
vertex ${(x+w).toFixed(2)} ${y.toFixed(2)} ${z.toFixed(2)}
vertex ${(x+w).toFixed(2)} ${(y+h).toFixed(2)} ${z.toFixed(2)}
endloop
endfacet
facet normal 1 0 0
outer loop
vertex ${(x+w).toFixed(2)} ${y.toFixed(2)} ${fromZ}
vertex ${(x+w).toFixed(2)} ${(y+h).toFixed(2)} ${z.toFixed(2)}
vertex ${(x+w).toFixed(2)} ${(y+h).toFixed(2)} ${fromZ}
endloop
endfacet
`;
};
scalePx = 0.4;
maxHeight = 1.5;
maxCurve = 250;
curvedPos = (x) => {
dist = canvas.width;
x = (x * 100 / canvas.width) * maxCurve / 100;
return {
x : Number((50 * Math.cos(Math.PI * (x * scalePx) / 180 )).toFixed(2)),
z : Number((50 * Math.sin(Math.PI * (x * scalePx) / 180 )).toFixed(2))
};
};
img.parentNode.removeChild(img);
curved = curvedPos(canvas.width);
tmpX = curved.x;
tmpZ = curved.z;
console.log(tmpX, canvas.width);
if (addSupportCheckbox.checked){
let tmpXArry = []
buff += createCube(0, tmpX, 0, tmpZ*scalePx, scalePx, (canvas.height+1)*scalePx);
for (var x = 0; x <= canvas.width; x+=0.1){
curved = curvedPos(x);
tmpX = curved.x;
tmpZ = curved.z;
keyLine = tmpX.toString().concat('---------', tmpZ);
if (tmpXArry.indexOf(keyLine) != -1) continue;
tmpXArry.push(keyLine);
buff += createCube((tmpZ * scalePx) - scalePx, tmpX, 0, tmpZ * scalePx, scalePx, (canvas.height+1)*scalePx);
}
}
for (var y = 0; y <= canvas.height; y++){
for (var x = 0; x <= canvas.width; x++){
//Curved
curved = curvedPos(x);
tmpX = curved.x;
tmpZ = curved.z;
data = canvas.ctx.getImageData(x, y, 1, 1)
color = data.data;
percentColor = ((255-((color[0]+color[1]+color[2])/3))*100/255);
z = maxHeight*(percentColor/100);
if (color[3] > 0 && z > scalePx){
buff += createCube(
(tmpZ*scalePx) - scalePx,
tmpX,
y*scalePx,
(tmpZ+z)*scalePx,
scalePx,
scalePx);
}
grey = ((100-percentColor) * 255 / 100);
for (var i = 0; i<=2;i++) data.data[i] = grey;
canvas.ctx.putImageData(data,x, y);
};
};
buff +="\nendsolid litophanie";
//console.log(buff);
downloadFile.href = URL.createObjectURL(new Blob([buff], {contentType:'text/csv'}));
downloadFile.target = 'BLANK'
downloadFile.download='lithographie.stl';
downloadFile.click();
};
html.textContent = '';
img = document.createElement('input');
img.type = 'file';
[ descriptionSupportCheckBox, addSupportCheckbox, document.createElement('p'),
descriptionMaxWidthInput, maxWidthInput, document.createElement('p'),
img, document.createElement('p')].map(el=>html.appendChild(el));
img.addEventListener('change', (e)=>{
let tmpImg = document.createElement('img'),
imgBlob = new FileReader();
html.appendChild(tmpImg);
tmpImg.setAttribute('style', 'width:250px');
tmpImg.addEventListener('load', generateAsciiStlLitophanie);
imgBlob.addEventListener('load', (evt)=>{
tmpImg.src = evt.target.result;
});
imgBlob.readAsDataURL(e.target.files[0]);
});Conclusion
Il existe aujourd’hui de nombreux outils qui vous permettent de faire de la Lithophanie sur tout type de support cylindre, sphère, cube, ….
L’objectif de cet article est purement pédagogique, à la fois pour permettre de « comprendre » comment cela fonctionne, mais aussi pour donner
un peu d’éclat aux « Mathématiques » appliqués aux développements logiciels, trop souvent négligé ou délaissé à des librairies, des frameworks…
Ici rien de complexe, des tableaux en croix, un peu de trigonométrie, et on récupère directement le fruit de cette compétence nouvellement acquise !
Histoire de faire, un peu de teasing, ces travaux sont issues d’un projet que je mène un peu en arrière plan, le Maker Campus 2026 sur
l’agglomération de Nantes. Pour l’instant, rien n’est acté, mais l’idée serait d’y avoir un stand et de vous exposer des petits objets ludiques sur cette
thématique Photo / animation / 3D, je vous donnerais davantage d’infos dans les prochains mois.
 Dyrk.org
Dyrk.org